因果发现最新进展及其在复杂系统中实践的探讨

摘要

在处理时序数据的因果关系时，检测两个变量之间的因果关系通常采用格兰杰因果关系。霍克斯过程是一种能描述复杂系统的点过程，广泛应用于社交网络分析、生物信息学、金融分析等多个领域。目前，在霍克斯过程中发现格兰杰因果关系是因果推断的重要研究内容，日益受到关注。本文分析当前因果推断技术的最新研究进展以及其应用于复杂故障诊断系统的工程实践，希望为致力于复杂系统中的因果发现的工程实践者提供一定的技术借鉴和参考。

背景

在处理时序数据的因果关系时，检测两个变量之间的因果关系通常采用格兰杰因果关系（Granger causality）。霍克斯过程（Hawkes process）是一种能描述复杂系统的点过程，广泛应用于社交网络分析、生物信息学、金融分析等多个领域。目前，在霍克斯过程中发现格兰杰因果关系是因果推断的重要研究内容，日益受到关注。

本文分析了当前因果推断技术的最新进展以及其应用于复杂系统中的故障诊断系统的工程实践。本文首先探讨了霍克斯过程及文[1]在多变量霍克斯过程中引入拓扑结构的设计思路和方法，其次，将之与同样用于连续时间因果关系建模的连续贝叶斯模型[2]进行对比，最后探讨了文[1]方法在工程实践上可能遇到的问题和挑战。本文希望借此探讨为致力于复杂系统中的因果发现的工程实践者提供一定的技术借鉴和参考。

霍克斯过程（Hawkes Process）

霍克斯过程是一种强度函数值依赖于历史事件的自激励点过程，其特征是其历史事件的影响以时间累加的形式进行。在霍克斯过程中一个重要的概念就是条件强度函数

，表示在单位时间内事件到达的平均速率。与一般的点过程不同的是，霍克斯过程的强度函数随着时间而变化，且其历史事件对未来事件的影响是单调指数递减，然后以累加形式进行叠加，其形式化定义如式（1）所示。其中

表示截止到时间

的所有历史事件，

是给定的确定性函数，

是核函数，描述了过去事件对当前事件的影响。也就是说，这是对在时间点

之前的所有事件都进行了考虑。为了描述这些影响随着时间的衰减效应，尤其是最新事件对未来事件的最大影响，核函数一般采用类似于指数函数的形式，但将标准的指数函数的一个参数演变为两个参数

、

，分别表示事件类型

对事件类型

的影响程度及衰减率，如式（2）所示。随着时间变化的强度函数

的实例如图1所示。

图1：变化的强度函数

（来源：文[3]）

作为点过程的变体，霍克斯过程也继承了点过程的基本语义。比如，图2中的随机变量

表示相邻两个事件起始时间之间的间隔，

表示事件发生的起始时间，如

表示在发生事件4的时间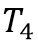

与发生事件5的时间

之间的时间间隔，并且这些时间间隔都服从一定的概率分布。

图2：点过程（来源：文[3]）

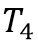
同时，截止到时间

事件发生的总次数表示为变量

，是一个右连续函数，如式(3)、图3所示。

图3：事件次数随机变量

（来源：文[3]）

拓扑结构的霍克斯过程(Topological Hawkes Process, TTPM)

标准霍克斯过程表示只有事件之间存在相互影响，事件并不受其他因素影响。这种假设没有考虑事件发生的物理结构，这往往会造成模型训练得到虚假、错误的因果关系。比如，假设现有三种事件类型

，这些事件发生在三个设备

，以及设备之间的拓扑结构

和事件类型的因果关系图

，如图4所示，该结构图表示

同时受设备

上的事件类型

影响。如果我们仅仅将观察数据按照时间序列进行训练而忽略设备之间的拓扑关系，会导致我们训练得到图5中的错误结构，由于忽略了

设备对时间

的影响，误认为

也是因果关系图中的一部分。换言之，也就忽略了设备

作为混淆变量的作用。正确的解读方式应该如图6所示。

图4：真实的因果图（来源：文[1]）

图5：错误的数据解读方式（来源：文[1]）

图6：正确的数据解读方式（来源：文[1]）

TTPM训练方法

在文献[1]中，模型训练主要采用了EM（Expectation Maximization）迭代算法来评估最好的模型参数，其主要思想是从没有任何连边的空图和随机参数开始，然后在当前最优图结构上进行一次的边增加、删除、reverse操作，得到当前图的邻居图。然后在这些邻居图中根据模型的似然值（Likelihood）找到比当前图更优的图，直到找不到为止，具体算法可参见[1]。

值得注意的是，该训练方法中由于使用了EM算法，也无可避免地具备EM迭代优化方法的计算属性。首先，EM算法可以保证收敛到一个稳定点，但是却不能保证收敛到全局的极大值，因此是局部最优算法。这跟算法的初始值有关，因此为确保结果的准确性和稳定性，运行时可以设置多个初始值。当然，当优化目标是凸函数时，可以保证收敛到全局最大值，这与梯度下降的迭代算法相同。由于是迭代优化算法，训练时间与效果往往跟实际经验相关，比如，超参数中迭代次数决定了运行时间，核函数中的衰减系数决定了算法效果，这也说明了工程能力或者说调参能力在算法实践中的巨大作用。此外，该训练方法与事件类型数量成平方阶关系，与EM的迭代次数一起，对计算成本提出了更大的需求。

总结与思考

作为霍克斯过程的演变模型，TTPM也只关注事件发生的时间点，而不管事件的持续时间，即事件间隔时间

由两个事件的起始时间所决定，而每个事件持续时间却是未知。在这方面，现有的连续贝叶斯模型[2]却能很好地捕捉事件的停留时间，这对实际建模可能存在很大的影响。因为现实中，往往数据包含持续时间信息，如图7所示的警报器的历史数据（end_timestamp – start_timestamp）。在模型训练过程中，从连续贝叶斯模型的角度来看，只需要从观察数据中获得足够的统计数据，即计算每个事件类型的持续时间和状态转变次数，而不像TTPM需要EM这样的迭代优化算法，其计算速度远远超过TTPM，这对算法设计节省了巨大的计算和时间成本。在算法性能上，TTPM有一定的优势。因此，也引出一个问题，针对计算成本低的连续贝叶斯模型，如何进一步提高其性能?

图7：基于观察的警报器数据（来源：文[4]）

同时，在复杂故障系统中，找出根故障节点可以为排除其他故障提供了解决方向。比如，系统中的两个警报器 A、B，如果警报器B是警报器A导致的，在解除了故障A多久之后故障B会自动解除？对于这样的问题，TTPM就不能很好解决。

当然，TTPM算法的性能严重依赖于BIC（Bayesian information criterion）惩罚因子、核函数中的衰减因子

等超参数，这对工程实践提出了较高的要求。与之相反，连续贝叶斯模型的性能就比较稳定。在实践工程中，我们也发现，通过对给定时间点进行一定的扰动，在一定程度上能改进连续贝叶斯模型的性能。最后，在数据缺失的情况下，如在图7中，如果alarm_id的起始时间缺失，TTPM只能通过删除该条数据，以便适应算法。当缺失数据在观察数据中占到一定比例时，这种抛弃信息的方法必然对TTPM不利。相反的，连续贝叶斯网络却可以不做任何处理就能适用。

由于水平有限，文中存在不足的地方，请各位读者批评指正，也欢迎大家参与我们的讨论。

参考文献

[1] Cai, Ruichu/ Wu, Siyu / Qiao, Jie / Hao, Zhifeng / Zhang, Keli / Zhang, Xi THP: Topological Hawkes Processes for Learning Granger Causality on EventSequences 2021

[2] Nodelman, Uri, Christian R. Shelton, and Daphne Koller. "Continuous time Bayesian networks." arXiv preprint arXiv:1301.0591 (2012).

[3] Rizoiu, Marian-Andrei, et al. "A tutorial on hawkes processes for events in social media." arXiv preprintarXiv: 1708.06401 (2017).

[4] https://competition.huaweicloud.com/information/1000041487/introduction

往期推荐

1、基于观察数据的因果推断

2、神经渲染最新进展与算法（一）：语义图像合成

3、病理AI：基于深度学习的方法综述