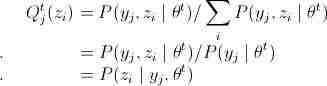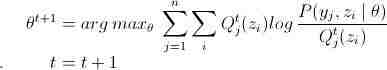在推导EM算法之前，先引用《统计学习方法》中EM算法的例子：
例1. (三硬币模型) 假设有3枚硬币,分别记作A,B,C。这些硬币正面出现的概率分别为π，p和q。投币实验如下，先投A，如果A是正面，即A=1，那么选择投B；A=0，投C。最后，如果B或者C是正面，那么y=1；是反面，那么y=0；独立重复n次试验（n=10)，观测结果如下： 1,1,0,1,0,0,1,0,1,1假设只能观测到投掷硬币的结果，不能观测投掷硬币的过程。问如何估计三硬币正面出现的概率，即π，p和q的值。
 解：设随机变量y是观测变量，则投掷一次的概率模型为：
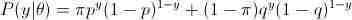
有n次观测数据Y，那么观测数据Y的似然函数为：

那么利用最大似然估计求解模型解，即：

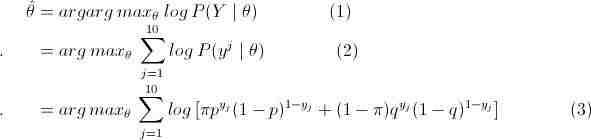
这里将概率模型公式和似然函数代入（1）式中，可以很轻松地推出 (1)=> (2) => (3)，然后选取θ(π,p,q)，使得（3）式值最大，即最大似然。然后，我们会发现因为（3）中右边多项式+符号的存在，使得（3）直接求偏导等于0或者用梯度下降法都很难求得θ值。
这部分的难点是因为（3）多项式中+符号的存在，而这是因为这个三硬币模型中，我们无法得知最后得结果是硬币B还是硬币C抛出的这个隐藏参数。那么我们把这个latent 随机变量加入到 log-likelihood 函数中，得
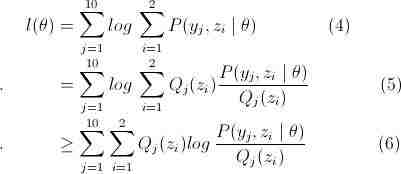
略看一下，好像很复杂，其实很简单，请容我慢慢道来。首先是公式（4），这里将zi做为隐藏变量，当z1为结果由硬币B抛出，z2为结果由硬币C抛出，不难发现
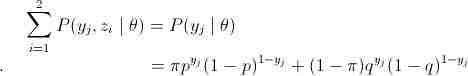
 接下来公式说明（4）=> （5）（其中（5）中Q(z)表示的是关于z的某种分布，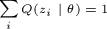
），很直接，在P的分子分母同乘以Q(zi)。最后是（5）=>（6），到了这里终于用到了第二节介绍的Jensen不等式，数学好的人可以很快发现，
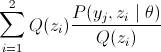就是
的期望值。且log是上凸函数，所以就可以利用Jensen不等式得出这个结论。因为我们要让log似然函数l(θ)最大，那么这里就要使等号成立。根据Jensen不等式可得，要使等号成立，则要使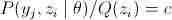
成立。
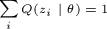
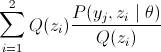
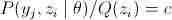
 再因为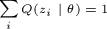
，所以得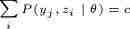
,c为常数，那么

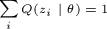
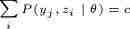
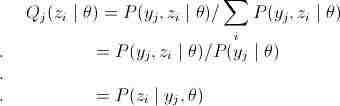
这里可以发现
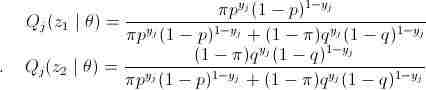
到这里，可以发现公式（6）中右边多项式已经不含有“+”符号了，如果知道Q(z)的所有值，那么可以容易地进行最大似然估计计算，但是Q的计算需要知道θ的值。这样的话，我们是不是可以先对θ进行人为的初始化θ0，然后计算出Q的所有值Q1(在θ0固定的情况下，可在Q1取到公式（6）的极大值)，然后在对公式（6）最大似然估计，得出新的θ1值（在固定Q1的情况下，取到公式（6）的极大值），这样又可以计算新的Q值Q1,然后依次迭代下去。答案当然是可以。因为Q1是在θ0的情况下产生的，可以调节公式（6）中θ值，使公式（6）的值再次变大，而θ值变了之后有需要调节Q使（6）等号成立，结果又变大，直到收敛（单调有界必收敛）。

在《统计学习方法》书中，进行两组具体值的计算

      （1）π0=0.5, p0=0.5, q0=0.5，迭代结果为π=0.5, p=0.6, q=0.5

      （2）π0=0.4, p0=0.6, q0=0.7，迭代结果为π=0.4064, p=0.5368, q=0.6432

    两组值的最后结果不相同，这说明EM算法对初始值敏感，选择不同的初值可能会有不同的结果，只能保证参数估计收敛到稳定点。因此实际应用中常用的办法就是选取多组初始值进行迭代计算，然后取结果最好的值。
EM算法
1.模型说明
考虑一个参数估计问题，现有
共n个训练样本，需有多个参数θ去拟合数据，那么这个log似然函数是：
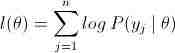
可能因为θ中多个参数的某种关系（如上述例子中以及高斯混合模型中的3类参数），导致上面的log似然函数无法直接或者用梯度下降法求出最大值时的θ值，那么这时我们需要加入一个隐藏变量z，以达到简化l(θ),迭代求解l(θ)极大似然估计的目的。
2.EM算法推导
这小节会对EM算法进行具体推导，许多跟上面例子的解法推导是相同的，如果已经懂了，可以加速阅读。首先跟“三硬币模型”一样，加入隐变量z后，假设Q(z)是关于隐变量z的某种分布，那么有如下公式：
公式（7）是加入隐变量，（7）=>（8）是在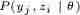
基础上分子分母同乘以
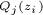，（8）=>（9）用到Jensen不等式（跟“三硬币模型”一样），等号成立的条件是
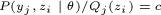，c是常数。再因为
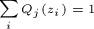，则有如下Q的推导：
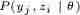
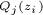
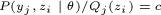
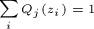
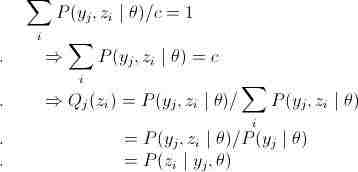
再一次重复说明，要使（9）等式成立，则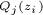
为yj,z的后验概率。算出
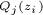后（9）就可以进行求偏导，以剃度下降法求得θ值，那么又可以计算新的
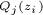值，依次迭代，EM算法就实现了。
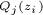
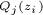
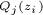
选取初始值θ0初始化θ，t=0
Repeat {
      E步：
      M步：
}直到收敛
EM算法的基本思路就已经理清，它计算是含有隐含变量的概率模型参数估计，能使用在一些无监督的聚类方法上。在EM算法总结提出以前就有该算法思想的方法提出，例如HMM中用的Baum-Welch算法就是。
主要参考文献
[1]Rabiner L, Juang B. An introduction to hidden markov Models. IEEE ASSP Magazine, January 1986，EM算法原文
[2]http://v.163.com/special/opencourse/machinelearning.html，Andrew NG教授的公开课中的EM视频
[3]http://cs229.stanford.edu/materials.html, Andrew NG教授的讲义，非常强大，每一篇都写的非常精炼，易懂
[4]http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html, 一个将Andrew NG教授的公开课以及讲义理解非常好的博客，并且我许多都是参考他的
[5]http://blog.csdn.net/abcjennifer/article/details/8170378, 一个浙大研一的女生写的，里面的博客内容非常强大，csdn排名前300
[6]李航.统计学习方法.北京：清华大学出版社，2012
继续阅读
阅读原文