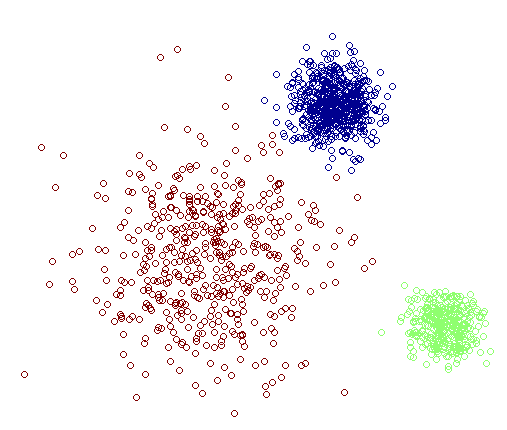
通过学习概率密度函数的Gaussian Mixture Model (GMM) 与 k-means 类似，不过 GMM 除了用在 clustering 上之外，还经常被用于 density estimation。对于二者的区别而言简单地说，k-means 的结果是每个数据点被 assign 到其中某一个 cluster ，而 GMM 则给出这些数据点被 assign 到每个 cluster 的概率。
作为一个流行的算法，GMM 肯定有它自己的一个相当体面的归纳偏执了。其实它的假设非常简单，顾名思义，Gaussian Mixture Model ，就是假设数据服从 Mixture Gaussian Distribution ，换句话说，数据可以看作是从数个 Gaussian Distribution 中生成出来的。实际上，一般在K-means 和 K-medoids 中所用的例子就是由多个Gaussian 分布随机生成的。实际上，从中心极限定理可以看出，Gaussian 分布这个假设其实是比较合理的，除此之外，Gaussian 分布在计算上也有一些很好的性质，所以，虽然我们可以用不同的分布来随意地构造 XX Mixture Model ，但是还是 GMM 最为流行。另外，Mixture Model 本身其实也是可以变得任意复杂的，通过增加 Model 的个数，我们可以任意地逼近任何连续的概率密分布。
每个 GMM 由 K 个 Gaussian 分布组成，每个 Gaussian 称为一个“Component”，这些 Component 线性加成在一起就组成了 GMM 的概率密度函数：
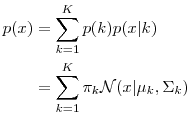
那么如何用 GMM 来做 clustering 呢？其实很简单，假定它们是由 GMM 生成出来的，那么我们只要根据数据推出 GMM 的概率分布来就可以了，然后 GMM 的  K 个 Component 实际上就对应了 K  个 cluster 。根据数据来推算概率密度通常被称作 density estimation 。
现在，假设我们有 N 个数据点，并假设它们服从某个分布（记作 p(x)），现在要确定里面的一些参数的值。 我们的想法是，找到这样一组参数，它所确定的概率分布生成这些给定的数据点的概率最大，而这个概率实际上就等于p(x)之和，我们把这个乘积称作似然函数 (Likelihood Function)。通常单个点的概率都很小，许多很小的数字相乘起来在计算机里很容易造成浮点数下溢，因此我们通常会对其取对数，把乘积变成加和 ，得到 log-likelihood function 。接下来我们只要将这个函数最大化（通常的做法是求导并令导数等于零，然后解方程），亦即找到这样一组参数值，它让似然函数取得最大值，我们就认为这是最合适的参数，这样就完成了参数估计的过程。
下面让我们来看一看 GMM 的 log-likelihood function ：
求解最大似然估计过程如下：
1. 估计数据由每个 Component 生成的概率（并不是每个 Component 被选中的概率）：对于每个数据 xi 来说，它由第 k 个 Component 生成的概率为
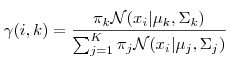
由于式子里的 方差 和 均值 也是需要我们估计的值，我们采用迭代法，在计算时将取上一次迭代所得的值（或者初始值）。
2. 估计每个 Component 的参数：现在我们假设上一步中得到的 r(i,k)  就是正确的“数据 xi 由 Component k 生成的概率”。集中考虑所有的数据点，现在实际上可以看作 Component 生成了所有的  这些点。由于每个 Component 都是一个标准的 Gaussian 分布，可以很容易分布求出最大似然所对应的参数值：
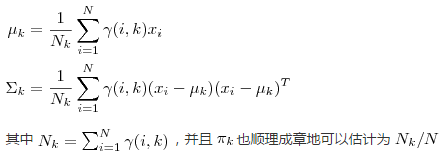
3. 重复迭代前面两步，直到似然函数的值收敛为止。
采用MATLAB自带的kmeansdata数据集进行验证仿真，具体代码如下所示。
%% 导入数据
load('kmeansdata')
%% 初始化混合模型参数
K = 3;

% 随机初始化均值和协方差
means = randn(K,2);
for k = 1:K

   covs(:,:,k) = rand*eye(2);
end
priors = repmat(1/K,1,K);   % 初始化，假设隐含变量服从先验均匀分布
%% 主算法
MaxIts = 100;   % 最大迭代次数
N = size(X,1);  % 样本数
q = zeros(N,K); % 后验概率
D = size(X,2);  % 维数
cols = {'r','g','b'};

plotpoints = [1:1:10,12:2:30 40 50];

B(1) = -inf;

converged = 0;

it = 0;

tol = 1e-2;
while 1

   it = it + 1; 
% 把乘除化为对数加减运算，防止乘积结果过于接近于0

   for k = 1:K

       const = -(D/2)*log(2*pi) - 0.5*log(det(covs(:,:,k)));

       Xm = X - repmat(means(k,:),N,1);

       temp(:,k) = const - 0.5 * diag(Xm*inv(covs(:,:,k))*Xm');       end

   % 计算似然下界

   if it > 1

 B(it) = sum(sum(q.*log(repmat(priors,N,1))))+  sum(sum(q.*temp)) - sum(sum(q.*log(q)));       
        if abs(B(it)-B(it-1))<tol

              converged = 1;        
          end

    end  

   if converged == 1 || it > MaxIts        
          break

   end

   % 计算每个样本属于第k类的后验概率

   temp = temp + repmat(priors,N,1);

   q = exp(temp - repmat(max(temp,[],2),1,K));


   q(q < 1e-60) = 1e-60;

   q(q > (1-(1e-60))) = 1-(1e-60);

   q = q./repmat(sum(q,2),1,K);    % 更新先验分布

   priors = mean(q,1);    % 更新均值

   for k = 1:K

       means(k,:) = sum(X.*repmat(q(:,k),1,D),1)./sum(q(:,k));    end

   % 更新方差

   for k = 1:K

       Xm = X - repmat(means(k,:),N,1);

       covs(:,:,k) = (Xm.*repmat(q(:,k),1,D))'*Xm;

       covs(:,:,k) = covs(:,:,k)./sum(q(:,k));

   end

end


%% plot the data

figure(1);hold on;


plot(X(:,1),X(:,2),'ko')
;for k = 1:K

  plot_2D_gauss(means(k,:),covs(:,:,k), -2:0.1:5,-6:0.1:6);
end
ti = sprintf('After %g iterations',it);

title(ti)
%% 绘制似然下界迭代过程图
figure(2);
hold off

plot(2:length(B),B(2:end),'k');

xlabel('Iterations');

ylabel('Bound');

继续阅读
阅读原文