请不要欺负
我们数学系
最近，小天发现了一个“有趣”的帖子：让数学系同学吐血的N种方法。
里面列举了整整10个梗来让我们数学系的同学们吐血！！
评论里面甚至还说我们数学系的不会算账，连数都不会数，只会数到3，因为1,2,3……n。
笑话！
这样黑我们数学系！这还得了！
于是，小天下定决心要代表数学系的同学们来“消灭”他们这群“黑友”！
①你能背圆周率多少位啊？你不会！？是不是数学系的啊
这个超模君在“π日”讲过啦（传送门），在评论区各位模友就不由自主地背了起来。。。
而小天想反问：为什么要背圆周率？会用就好了嘛。。。
②怎么画正十七边形啊？你不会！？是不是数学系的啊
对于画正十七边形，各位模友表示都会画！（传送门）
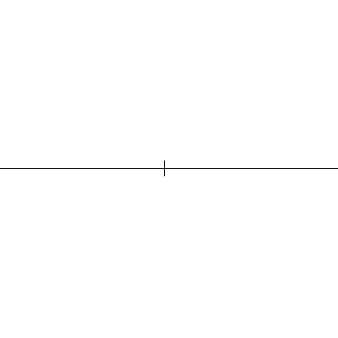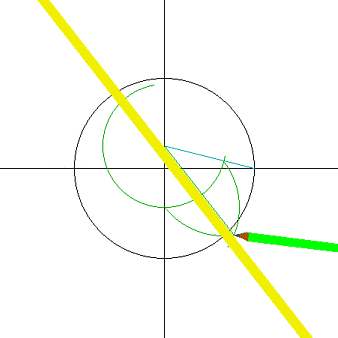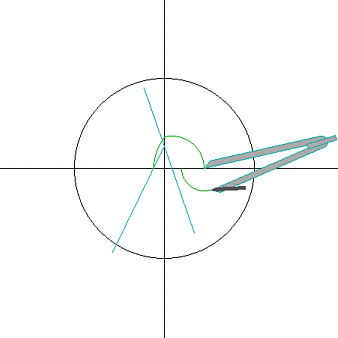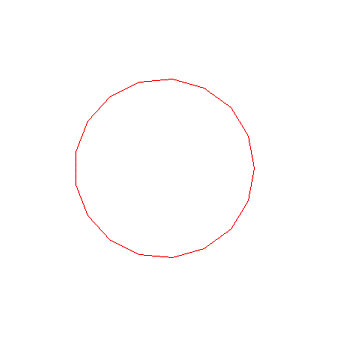
③你们玩牌没输过吧！你输过！？是不是数学系的啊
我最近不玩牌，我只玩硬币。。。
如何制定一个必赢的赌博规则（传送门）。
④3D心形的函数（用词！）是什么啊？你不会！？是不是数学系的啊
谁说我不会！

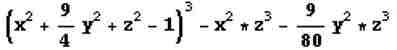
⑤三个人住旅馆……少的一元钱去哪了？
有3个人去入住京西旅馆，每人每晚需要10元，共30元。于是小天向他们每人收了 10 元。
后来，刘老板心情好，想给他们点优惠，于是对小天说：今天优惠只要25元就够了，你将这5元退还给他们3个吧。
小天想：5元怎么能退回给3个人呢？既然今天强西老板如此高兴，那赏我2元也是可以的。。
于是，小天就收好了2元，然后将3元分别退还给了3为旅客。
一切都看似很正常，但是，请你看看以下计算：
一开始每人掏了10元，现在又退回1元，也就是10-1=9,，每人只花了9元钱，3个人每人9元，3 X 9 = 27元 + 小天自己收好的2元=29元。。。
还有 1 元钱去了哪里???
完全就是两个不同的概念，而且超模君已经讲过，少的那一元就在这里：那些年我们被骗过的题目（传送门）。
⑥0.999999…为什么等于1？
简单的证明：
1/3 用小数表示为 0.33333……
0.33333……乘3得0.9999……
1/3 乘 3 = 1 
所以，0.9999……=1
稍微复杂的证明：

令 x = 0.999……

所以 10x = 9.999……

两式相减得 9x = 9

所以 x = 1
最复杂的证明：


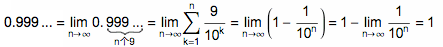
⑦为什么奇数和整数一样多？
整数有无穷多个，奇数也有无穷多个。
一般而言，两个无穷多的集合是不比较多少的。
但是也可以用集合的观点来看集合的元素的个数的“多少”。
主要是在两个集合的元素之间建立对应关系，如果能够一个对一个的对应，就说二者的元素一样多，如果无论如何都不能建立这样的一对一的关系才说二者的元素不一样多
整数和奇数之间的关系：
每一个奇数都可以通过加上1，再除以2得到一个整数。
这样的话，每一个奇数都对应一个整数。
因此，奇数的全体和整数的全体之间可以建立一一对应的关系。
所以可以说整数和奇数的个数一样多：
（1，1）（3，2）（5，3）……（99，50）……（2n-1，n）……
⑧你家有克莱因瓶吗？你没有！？是不是数学系的啊
1882年，德国数学家菲利克斯·克莱因提出了克莱因瓶的概念。
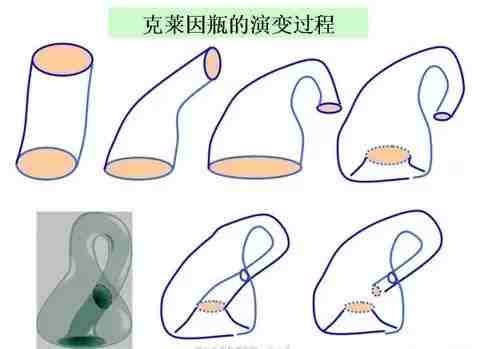
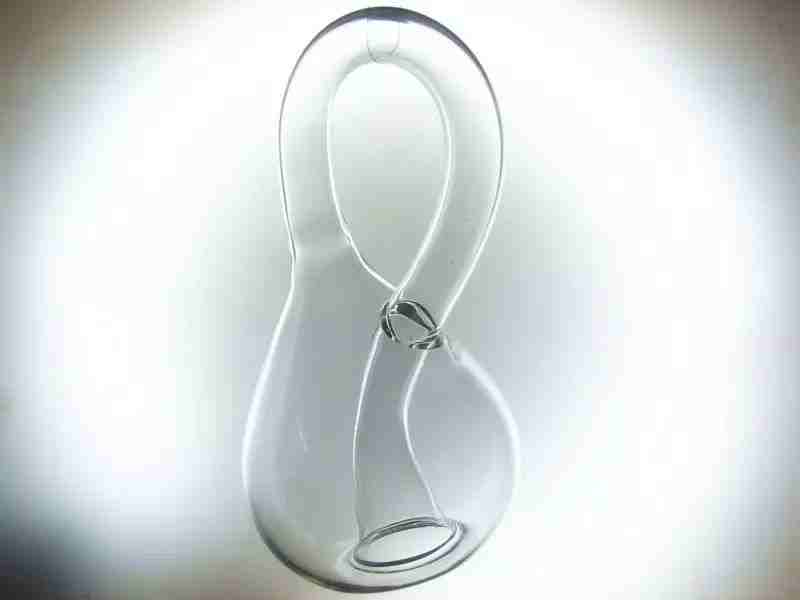
克莱因瓶其实不是“瓶”，是一种不可定向的二维紧致流形，没有内外部之分。比如说一只苍蝇可以从瓶子的内部直接飞到外部而不用穿过表面。
事实上，克莱因瓶是一个在四维空间中才可能真正表现出来的曲面，我们生活的三维空间是无法将它完全表现出来的。
在三维空间中，我们只能做出“浸入”模型(允许与自身相交)，比如：一个瓶子底部有一个洞，延长瓶子的颈部，并且扭曲地进入瓶子内部，然后和底部的洞相连接。
所以，我们为什么要弄个“将就”版的克莱因瓶呢？
⑨你知道四维空间什么样吗？你不知道！？是不是数学系的啊
四维空间要靠自己想象的，恕我无法告诉你。。。

⑩这个七阶魔方怎么复原？你不会！？是不是数学系的啊

7阶魔方算什么，现在流行的是“丧心病狂”的13阶魔方！
所以啊
不要轻易欺负我们数学系的
因为厉害起来连我们自己都怕
本文由超级数学建模编辑整理
部分资料来源于网络
转载请在公众号中，回复“转载”
-----这里是数学思维的聚集地------
“超级数学建模”（微信号supermodeling），每天学一点小知识，轻松了解各种思维，做个好玩的理性派。30万数学精英都在关注！
商务合作请加微信zwz2434
继续阅读
阅读原文