作者：石川，北京量信投资管理有限公司创始合伙人，清华大学学士、硕士，麻省理工学院博士。
封面来源：https://www.pexels.com
未经授权，严禁转载。
摘
要
本文介绍三种常见的以控制族错误率为目标的多重检验算法，并给出基于 A 股市场异象的实证分析。
00
引言
近日，长期战斗在抵制金融学领域虚假发现一线的 Campbell Harvey 教授和他的 co-authors 在 Review of Asset Pricing Studies 上发表了一篇关于多重假设检验方法的综述性文章（Harvey, Liu, and Saretto 2020）。
该文系统的梳理了常见的控制多重检验、计算 t-statistic 阈值的方法，并给出了 code（虽然是 Matlab……）。凭借丰富的经验，三位学者在文中也给出了在研究金融学问题（例如异象研究或者基金选择）时如何选择方法的建议，极具实践意义。
鉴于多重检验问题日益严峻，我决定给《出色不如走运》开个“番外篇”，就叫《常见多重检验方法及其实证》系列。本文是这一系列的第 (I) 篇，介绍以控制族错误率为目的的算法，并针对 A 股中的代表性异象给出实证结果。
下文的行文顺序为：第一节简要介绍基础知识，包括多重假设检验和 stationary bootstrap，后者是一大类多重检验算法的基础；第二节讨论三种多重检验算法；第三节介绍实证结果；第四节给出金融学应用建议。
01
基础知识
1.1 多重假设检验
多重假设检验问题公众号已经介绍了很多了（见《出色不如走运》系列），本小节仅简单说明。
使用同样的数据同时检验多个原假设就是统计学中的多重假设检验（multiple hypothesis testing，简称 MHT 问题）。以研究异象为例，对着同样的历史数据挖出成百上千个异象就是多重假设检验问题。
MHT 问题的存在使得单一检验的 t-statistic 被高估，即里面有运气的成分。当排除了运气后，该异象很可不再显著。如果仍然按照传统意义上的 2.0 作为 t-statistic 阈值来评价异象是否显著，一定会有很多伪发现（false discoveries 或 false rejections）。因此，排除 MHT 影响的核心就是控制伪发现发生的概率。以此为目标，很多不同的多重检验算法被提出。学术界提出的不同算法可以分为三大类，借助下表说明。
假设一共研究了 S 个异象，其中 S_0 个在原假设下为真（即收益率为零），S_1 个在原假设下为假（即收益率不为零）。假设根据事先选定的显著性水平（通常为 5%），有 R 个假设被拒绝了，而其中包括 F_1 个 false rejections（因为它们的原假设为真）。
使用 F_1 和 R 可以定义一些不同的统计量，而不同的 MHT 算法是以控制不同的统计量为目标。这些统计量包括三大类，分别为族错误率（family-wise error rate，FWER）、伪发现率（false discovery rate，FDR）和伪发现比例（false discovery proportion，FDP）。它们都是描述一类错误，即错误拒绝原假设的统计量。
族错误率（FWER）的定义是出现至少一个伪发现的概率，即 prob(F_1 ≥ 1)。在给定的显著性水平 α 下，控制它的数学表达式为：
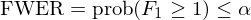
由定义可知，FWER 对单个假设非常严格，会提升二类错误的数量，削弱检验的 power。常见的算法包括 Bonferroni 和 Holm 方法，以及 White (2000) 的 bootstrap reality check 算法，Romano and Wolf (2005) 的 StepM 算法和 Romano and Wolf (2007) 的 k-StepM 算法。早在《出色不如走运(II)?》一文我们就介绍了 Bonferroni 和 Holm 方法。本文的目标是介绍后三种方法。
伪发现率（FDR）的定义为 E[F_1/R]。在给定的水平 δ 下，它可以表达为：
从定义可知，FDR 允许 F_1 着 R 的增大而成比例上升，是一种更加温和的方法。常见的算法为 BHY 方法（见《出色不如走运(II)?》）。
最后，伪发现比例（FDP）以限制 F_1/R 超过给定阈值 γ 的概率不超过给定的显著性水平 α 为目标：
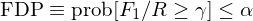
和 FDR 类似，它也允许 F_1 随 R 增加，因而比 FWER 更加温和。其中著名的算法包括 Romano and Wolf (2007) 以及 Romano, Shaikh, and Wolf (2008)。
1.2 自助法
本文的目标是介绍 bootstrap reality check、StepM 以及 k-StepM 三种控制 FWER 的算法。这三种算法的优点是不对数据的分布做任何假设，因为它们都依赖于 bootstrap 自助法进行重采样，并在此基础上结合正交化求出 t-statistic 的阈值。
对于研究异象来说，由于绝大多数变量都是高度相关的，因此异象的收益率也是高度相关的。为了保留时序和截面上的相关性，在进行重采样时，往往采用 block bootstrap。顾名思义，block bootstrap 就是每次从序列中有放回的抽取一个由连续 n 个相邻数据点构成的 block（大小由 block size 决定）。主流的 block bootstrap 算法包括以下三种：moving block bootstrap，circular block bootstrap 以及 stationary bootstrap。
关于自助法更详细的介绍请见《使用正交化和自助法寻找显著因子》一文。本文将遵循学术界的选择，使用 Politis and Romano (1994) 提出的 stationary bootstrap 算法进行重采样。
02
三种控制 FWER 算法
本节介绍的三种算法的核心都是“正交化”+“自助法”。“正交化”可以理解为人为消除异象变量和收益率之间的任何关联。正交化之后，我们就可以把该变量看成是随机的，因而正交后异象的收益率也仅仅是来自运气。“自助法”则是为了得到仅因运气成分而造成的统计量的分布，以此就可以判断原始异象变量的显著性是否是真实的，还是仅仅是运气。
值得一提的是，这三种算法本身也是密切相关的，后一个站在前者的基础之上。下文将以异象月均收益率的 t-statistic 作为统计量，介绍不同的算法。
为了方便地介绍三种算法，先来做一些铺垫工作。假设一共有 M 个异象，原始数据为 T × M 阶收益率序列矩阵（记为 D），其中 T 为月频期数，M 为异象的个数。首先，对每个异象计算月均收益率的 t-statistic，得到一个 M 阶向量，记为 θ。
接下来，使用 stationary bootstrap 算法对原始矩阵 D 重采样 B 次。对每一个 bootstrap sample，计算 M 个异象的 bootstrapped t-statistics 并取绝对值。由于在重采样时并没有强加“正交化”，因此在计算异象 bootstrapped t-statistics 的时候就要应用“正交化”。
为此，对于给定 bootstrap sample 中的每个异象，计算该异象在当前 bootstrap sample 中的月收益率均值和标准差，使用该月均收益率均值减去原始数据 D 中该异象的月均收益率（这个减法正是“正交化”），然后将差值再除以前述标准差，就得到该异象在当前 bootstrap sample 中的 bootstrapped t-statistic。上述过程的数学公式为：
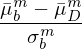
式中上标 m 代表第 m 个异象，下标 b 代表第 b 个 bootstrap sample，下标 D 代表原始数据。
依照上述操作，对于每一个 bootstrap sample，得到一个 M 阶经正交化调整后的 bootstrapped t-statistics 向量。由于一共有 B 次重采样（即 B 个 bootstrap samples），因此上述步骤得到的是 M × B 阶矩阵，其中每一行代表一个异象，每一列代表一次重采样，每个元素都是一个 bootstrapped t-statistic。称该矩阵为 Z。
向量 θ 和矩阵 Z 就是以下三种算法的输入。
2.1 Bootstrap Reality Check
将 M 个异象按它们月均收益率 t-statistics 的绝对值从高到低排列。Bootstrap reality check（BRC）算法的目标是检验排名第一的异象是否在考虑了 MHT 问题后依然显著。BRC 算法是 stationary bootstrap 的直接应用，非常直截了当，分为以下几步：
1. 对矩阵 Z 的每一列（即某个 bootstrap sample 下 M 个异象的 bootstrapped t-statistics）中 t-statistics 取绝对值并求出最大值；
2. 在上述得到的 B 个（因为一共有 B 个 bootstrap samples）最大值中，求出其 1 – α 分位数，这就是给定显著性水平下仅靠运气得到的最优 t-statistic 的阈值；
3. 比较 M 个异象中原始 t-statistic 的最大值是否超过上述阈值，如果超过，则其在 α 水平下显著。
值得一提的是，虽然很可能有多个异象的原始 t-statistics 超过了 BRC 算法给出的阈值，但 BRC 算法设计的初衷仅仅是为了检验 t-statistic 最高的异象是否依然显著，即它只关心所有异象中最显著的那一个。因此在所有 M 个异象中，该算法最多只拒绝一个原假设。毫无疑问，这太过苛刻。
2.2 StepM
StepM 是 BRC 的自然延伸。与 BRC 相比，它允许更过的原假设在 prob(F_1 ≥ 1) ≤ α 的前提下被拒绝，因此提高了检验的 power。StepM 算法具体包括以下三步：
1. 与 BRC 的前两步一样，计算 max bootstrapped t-statistic 的阈值（记为 c_1）。假设 M 个异象中，有 P_1 个的原始 t-statistics 超过 c_1，即这 P_1 个原假设在考虑了 MHT 后依然可以被拒绝，挑出这 P_1 个异象（它们被认为是真正异象）。剩余 M – P_1 个异象，它们的 t-statistics 小于 c_1。
2. 对于剩余的 M – P_1 个异象，在 Z 矩阵中找到它们所在的行，得到矩阵 Z’，以此为对象选出新一轮的 max bootstrapped t-statistic 阈值（记为 c_2）。假设在剩余异象中，有 P_2 个异象的 t-statistics 超过了 c_2，则认为它们的原假设也可以被拒绝，它们也被认为是真正的异象。此时，剩余 M – P_1 – P_2 个异象。
3. 重复上述第 2 步（每次新的迭代，对象都是剩余的 M – P_1 – P_2 – … – P_{j-1} 个异象），反复在剩余异象中求出新的（也是逐渐降低的）max bootstrapped t-statistic 阈值，直至无法挑出任何原始 t-statistics 不低于 c_j 的异象。最终，经过多次迭代的过程中，根据不同 max bootstrapped t-statistic 阈值（c_1、c_2 等）依次挑出的全部异象就是真正的异象。
2.3 k-StepM
虽然 StepM 比 BRC 方法允许更多的原假设被拒绝，但它依然比较苛刻。究其原因，还是因为 prob(F_1 ≥ 1) ≤ α 这个条件太严格 —— 它控制至少出现一个伪发现的概率。在 BRC 和 StepM 的算法中，上述条件体现为在每个 bootstrap sample 中，我们挑出了所有 M 个异象 t-statistics 绝对值的最大值，然后通过 B 个最大值得到其 1 – α 分位数作为阈值。
如果想要放松上述限制，就要从 prob(F_1 ≥ 1) ≤ α 入手。k-StepM 算法将其改为不少于 k 个伪发现的概率（这也是其得名的原因），即：
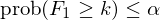
由定义可知，StepM（默认 k = 1）是 k-StepM 的一个特例。k-StepM 同样分为三步：
1. 对矩阵 Z 的每一列中 t-statistics 取绝对值并找到第 k 大的（注意，这里和 BRC 以及 StepM 最大的区别就是不再从每列取最大的 t-statistics 而是找到第 k 大的）；求 B 个第 k 大的 1 – α 分位数，这就是第一轮的阈值，记为 c_1；假设 M 个异象中，有 P_1 个的原始 t-statistics 超过 c_1，M – P_1 个小于 c_1。
2. 从 P_1 个异象中挑出 k – 1 个（这是一个组合问题，比如 5 选 3， 10 选 4 这种，我们这里是 P_1 选 k - 1），假设一共有 h 种方法。对于每种组合方法选出的 k – 1 个异象，进行如下操作：
2a. 将它们和剩余的 M – P_1 个异象放在一起，构成 M – P_1 + (k-1) 个异象的集合；
2b. 在 Z 矩阵中找到这 M – P_1 + (k-1) 个异象所在的行，得到矩阵 Z’，以此为对象找到第 k 大的阈值 c_2’；
取 h 种组合方法所得到的 h 个 c_2’ 的最大值，记为 c_2，这就是第二轮的阈值。从 M – P_1 个异象中，找出所有原始 t-statistics 高于 c_2 的异象（假设有 P_2 个）。
3. 重复上述第二步，只不过在每次迭代中挑选 k – 1 个异象的池子变为在之前迭代中已经被选出的异象（比如在第二次迭代中，池子是 P_1 个异象；在第三次迭代中，池子是 P_1 + P_2 个异象，以此类推）；反复计算出新一轮第 k 大 t-statistic 的阈值 c_j，直至无法挑出任何原始 t-statistics 不低于 c_j 的异象。
以上就是 k-StepM 的步骤。直观地说，它和 StepM 很接近 —— StepM 每次迭代用剩余异象的 Z’ 矩阵挑出最高 t-statistic 的分位数作为阈值；k-StepM 每次迭代用剩余异象的 Z’ 矩阵挑出第 k 高的 t-statistic 的分位数作为阈值。这是它们相似的地方。
然而，它们最大的区别在于，在 StepM 中，已经被选出的异象不会被重新考虑；而在 k-StepM 中，已经被选出的异象中的 k – 1 个会被重新考虑（和尚未被选出的一起作为剩余异象）。
“
One crucial aspect of the k-StepM procedure is the fact that, at each step, the critical value is calculated by reconsidering some of the strategies that have already been rejected.
”
这么做的原因和每次计算阈值时选择第 k 大的 t-statistic 以及该算法允许最多出现 k – 1 个伪发现有关。其假设在 j – 1 次迭代之后被拒绝的 P_1 +… + P_{j-1} 个异象中，有 k – 1 个伪发现。由于不知道其中的哪些是伪发现，因此该算法考虑了从 P_1 +… + P_{j-1} 中选出 k – 1 个的全部组合方式。
03
实证研究
为了说明上述三种方法的差异，本节针对 A 股中的 35 个异象做简单实证。这些异象均是常见的基本面或技术面异象，实证窗口为 2000 年 1 月 1 日至 2019 年 12 月 31 日。这些异象月均收益率的 t-statistics 由高到低如下表所示。
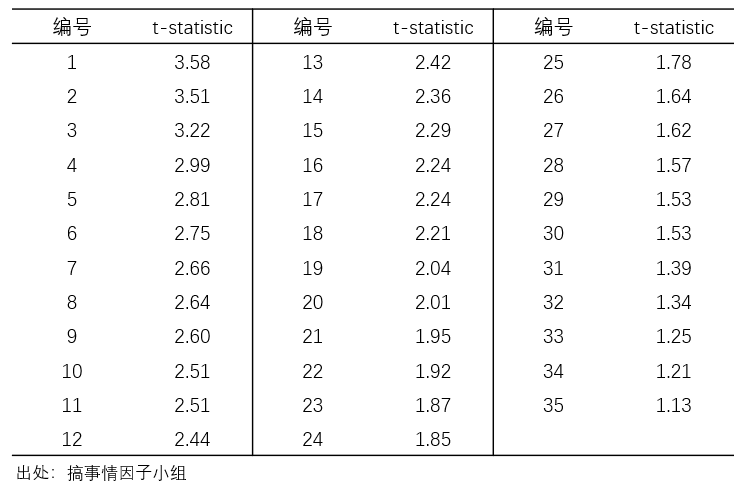
在实证中，进行 B = 1000 次 stationary bootstrap 重采样（令 block size 均值为 4；我验证了不同的取值，结果较为稳健），并计算上述 35 个异象的 Z 矩阵；并选择显著性水平 α = 5%。接下来看三种方法的实证结果。
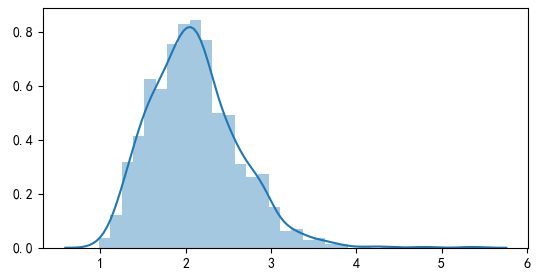
首先来看 BRC。利用 Z 矩阵，求出 max bootstrapped t-statistic 的分布（下图）以及 95% 的分位数为 2.98。由于 BRC 只关心 t-statistic 最高的异象，我们只需检验该值是否大于阈值。由于 3.58 大于 2.98，因此可以说在考虑了 MHT 后，该异象依然在 5% 的显著性水平下显著。（BTW，排名第一的异象是一个 SUE 类的异象。）
接下来看 StepM 算法。由于其第一次迭代和 BRC 一样，因此第一个阈值仍然是 2.98。在 35 个异象中，有 4 个超过了该阈值，因此被选出（其中有两个 SUE 类的异象，另外两个是市值和特质性动量）。在第二次迭代中，以剩余 31 个异象的 Z’ 矩阵为目标，算出的阈值为 2.93，因此未能选出新的异象。最终 StepM选出 4 个异象（来自第一次迭代），过程如下表所示。
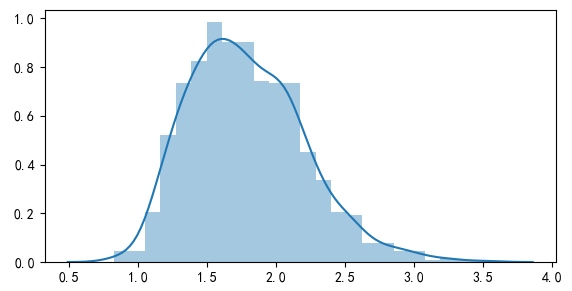
最后来看 k-StepM。实证中选择 k = 2。在第一次迭代中，第 2 大 bootstrapped t-statistic 的分布如下图所示，其 95% 分位数为 2.53。以此为阈值，前 9 个异象被选出（包括市值、ILLIQ、异常换手率、特质性动量以及三个 SUE 类等）。
在第二次迭代中，首先从上述 9 个异象中选出 1 个和剩余 26 个合并，以这 27 个异象的 Z’ 矩阵为目标计算出新的阈值；由于 9 选 1 一共有 9 种方式，因此上述过程共得到 9 个新的阈值，将它们的最大值作为本次迭代的阈值，该值为 2.41。以此为阈值，又有额外 4 个异象（异象 10 ~ 13）被选出。
在第三次迭代中，首先从前两次迭代选出的总共 13 个异象中选出 1 个和剩余 22 (= 35 - 13) 个合并，以这 23 个异象的 Z’ 矩阵为目标计算出新的阈值；由于 13 选 1 共有 13 种方式，因此上述过程共得到 13 个新的阈值，将它们的最大值作为本次迭代的阈值，该值为 2.34。以此为阈值，本次迭代选出异象 14。
在接下来的迭代中，由于没有新的异象被进一步选出，因此算法结束。通过三次迭代，k-StepM 算法共选出 14 个异象，过程如下表所示。
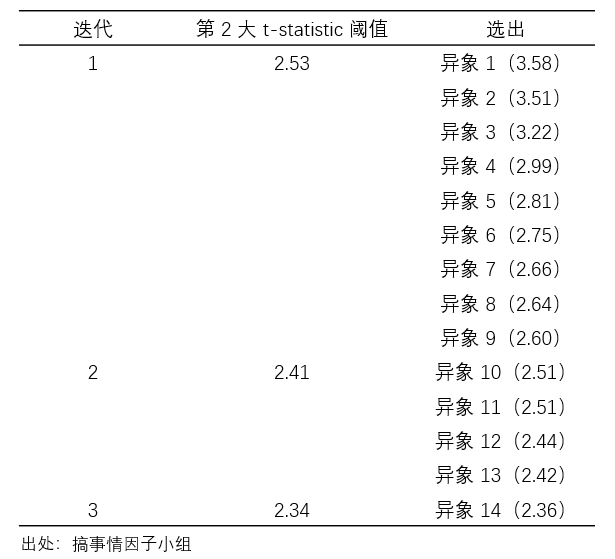
实证结果表明，k-StepM 放松了 StepM 对 FWER 的限制，因此有更多的原假设被拒绝。
04
金融学应用建议
本文介绍了三种常见的以控制 FWER 为目标的多重检验算法；它们只是众多算法的冰山一角。面对如此丰富的工具箱，选择合适的工具也就成为了难题 —— 算法是否合适很大程度上取决于数据满足怎样的假设。为此，Harvey, Liu, and Saretto (2020) 给出了一般性建议。
首先，原假设的个数（即异象的个数）是一个重要的选择依据。由于 FWER 类的算法非常严格，因此当 M 很大时，这类算法就不太合适，而应该选择以控制 FDR 或 FDP 为目标的算法。但如果检验的个数较少，比如 M = 10，选择此类算法则没有太大问题。
另一个需要考量的因素是不同原假设（异象）之间的相关性，即数据的相关性。当数据中存在很高的相关性时，依赖 bootstrap 的算法则比较适合。在这方面，本文介绍的三种算法，以及同样是 Romano and Wolf (2007) 提出的另一种控制 FDP 的算法（称为 FDP-StepM）则有一定的用武之地。
当我们手中有全新的样本时（比如其他国家的股市，或者不同时期的数据），Harvey, Liu, and Saretto (2020) 建议使用以控制 FDR 为目标的多重检验算法。由定义可知，FDR 是 FDP 的期望，较后者而言，它更加温和一些。
最后，如果上述 guideline 仍然无法让人选出合适的算法，我们也可以尝试 Harvey 教授的另一个大招 —— Harvey and Liu (2020)。用二位作者自己的话说：
“
They present a double bootstrap approach that delivers a set Type I error rate in multiple testing applications. Their method is data dependent so the cutoff will differ conditional on the particular data at hand. The method also allows the researcher to inject their prior on the proportion of hypotheses that are true. Finally, in contrast to other methods that focus on Type I errors, Harvey and Liu’s method allows the research to develop a decision framework that assigns differential costs of Type I and Type II errors.
”
怎么样？这篇即将发表在 Journal of Finance 的文章听上去就令人兴奋。我们以后找机会再细说。
参考文献
Harvey, C. R. and Y. Liu (2020). False (and missed) discoveries in financial economics. Journal of Finance forthcoming.
Harvey, C. R., Y. Liu, and A. Saretto (2020). An evaluation of alternative multiple testing methods for finance applications. Review of Asset Pricing Studies 10(2), 199 – 248.
Politis, D. N. and J. P. Romano (1994). The stationary bootstrap. Journal of the American Statistical Association 89(428), 1303 – 1313.
Romano, J. P., A. M. Shaikh, and M. Wolf (2008). Formalized data snooping based on generalized error rates. Econometric Theory 24(2), 404 – 447.
Romano, J. P. and M. Wolf (2005). Stepwise multiple testing as formalized data snooping. Econometrica 73(4), 1237 – 1282.
Romano, J. P. and M. Wolf (2007). Control of generalized error rates in multiple testing. The Annals of Statistics 35(4), 1378 – 1408.
White, H. (2000). A reality check for data snooping. Econometrica 68(5), 1097 – 1126.
免责声明：文章内容不可视为投资意见。市场有风险，入市需谨慎。
川总写量化
分享量化理论和实证心得
继续阅读
阅读原文