作者：石川，北京量信投资管理有限公司创始合伙人，清华大学学士、硕士，麻省理工学院博士。
封面来源：https://www.pexels.com
未经授权，严禁转载。
摘
要
贝叶斯思维和对 Type II error rate 的考量让多重假设检验方法上升到了新的高度。
01
引言
如果要说 2020 年令人印象深刻的金融学论文，Harvey and Liu (2020) 一定会有一席之地。在这篇题为 False (and missed) discoveries in financial economics、发表于 Journal of Finance 的文章中，二位作者将 multiple hypothesis testing（多重假设检验）方法论提升到了新高度。
如今再谈到多重假设检验，公众号的小伙伴一定不再陌生了。《出色不如走运》系列的前几篇文章均围绕这个话题进行了探讨。在学术论文方面，Harvey, Liu, and Saretto (2020) 一文对常见的方法进行了总结，而《出色不如走运》系列的“番外篇”《常见多重检验方法及其实证》也参照该文针对 A 股对其中一些方法进行了实证。
概括来说，传统的多重假设检验方法均可以归纳到“正交化” + “bootstrap”两个技术的综合运用。以挖掘股票市场异象为情景来说，其中“正交化”的作用是在样本内剔除每个异象的超额收益；“bootstrap”则是在正交化后的基础上通过重采样更多的数据，以此获得仅由运气造成的异象超额收益显著性（t-statistic）的分布。
在得到由运气造成的显著性（t-statistic）的分布后，这些方法往往以控制事先约定的 Type I error rate（false discovery rate），例如常见的 5%，来选定 t-statistic 的阈值，并以此确定哪些异象能够获得显著的超额收益。
传统方法虽然简单易用，但是存在两个问题：
1. 在“正交化”的过程中，往往会对所有异象都做“正交化”处理（原假设为异象超额收益为零）。然在现实中，这种处理方法忽视了先验的作用。对于待检验的诸多异象，人们可能根据金融学先验认为其中一定比例的异象的超额收益是显著的，但传统的方法并不能利用这种先验。
2. t-statistic 阈值是通过事先约定的 Type I error rate 确定的，而不去考虑 Type I 和 Type II 两类错误的 trade-off。这么做的结果是，传统多重假设检验方法的 Type II error rate 往往很高，power (= 1 – Type II error rate) 往往很低。举个极端的例子，假设某个算法把所有原假设都接受了，那么它也就没能发现任何真正的异象（power = 0）。
对研究异象来说，Type II error 意味着异象本身能够获得超额收益（原假设为假），但是检验并没有拒绝其原假设，因此错失了真正的异象。
尽管如此，常见方法仅仅关心 Type I error rate 也实在是无奈之举。这是因为哪怕对于单一假设检验，计算 Type II error rate 都并不容易，更不用说多重假设检验问题。如果想要计算 Type II error rate，就必须知道备择假设下参数的取值（本文附录部分引用了 Wikipedia 的例子说明如何在单一假设检验下计算 Type II error rate）。但显然，对于成百上千个异象来说，想要遍历它们备择假设下的预期超额收益不切实际。这个巨大的障碍使得人们难以将单一检验中计算 Type II error rate 的方法复制到多重假设检验问题中。
除了分析的难度，还有另一个原因是人们在过去通常认为 Type II error 的影响不如 Type I error 的影响大。以大幅提升分析难度为代价，换来的边际期望收益却有限，似乎有些得不偿失。不过，这种看法也逐渐在转变。在 α 越来越稀缺的当下，Type II error 的成本越来越高，让人开始重视两类错误之间的取舍。
在这种背景下，Harvey and Liu (2020) 提出了一个基于双重 bootstrap 的多重假设检验框架，同时解决了上述两个问题。
02
Harvey and Liu (2020)
假设一共有 N 个异象，原始数据为 T × N 阶异象收益率序列矩阵（记为 X_0），其中 T 为期数。这一步的设定和传统多重假设检验方法无异，但是 Harvey and Liu (2020) 的不同之处是通过参数 p_0 来控制真实异象的比例。人们可以根据自身的经验来选择 p_0 的取值，它是贝叶斯思维的体现。
当选定 p_0 后，一个自然的想法是在全部 N 个异象中收益率均值的 t-statistic 最高的 N × p_0 个是真实的。但是我们手头这 N 个异象的收益率序列也是来自未知总体。考虑到 sampling uncertainty，它们中最高的 N × p_0 个也并非就一定都是真的。为了解决这个问题 Harvey and Liu (2020) 进行了第一轮 bootstrap。
通过对 X_0 进行 bootstrap sampling 得到矩阵 X_i（下标 i 表示第 i 个 bootstrap 样本）。使用 X_i 中的收益率序列计算 N 个异象的 t-statistics，并选出最高的 N × p_0 个。在原始矩阵 X_0 中，将这些异象的收益率均值替换为它们在 X_i 中的均值，并把 X_0 中剩余那些异象的收益率做去均值处理，以此构造出矩阵 Y_i。
经过上述构造后，每次对 X_0 进行一次 bootstrap sampling，都会得到一个 Y_i，其中有 N × p_0 个异象的超额收益均值非零（显著的），剩余 N × (1 - p_0) 个异象的超额收益均值为零（不显著）。
在上述过程中，对剩余 N × (1 - p_0) 个异象时序收益率的去均值操作体现了“正交化”的思想；而对 N × p_0 个异象保留收益率均值则源于先验。此外这种操作通过单一参数 p_0 指定了原假设应被拒绝的异象，巧妙的绕过了后续计算 Type II error rate 时需要指定异象收益率参数的困难。
通过第一轮 bootstrap 得到的众多 Y_i 就是第二轮 bootstrap 的原始数据。对于每个 Y_i，其构造方法保证了我们知道哪些异象是真实的，哪些异象是虚假的，因此通过对 Y_i 进行 bootstrap sampling 就可以方便的计算 Type I 和 Type II error rates。
在 Y_i 的第 j 次 bootstrap 样本中，定义如下四个变量：
TN^{i, j}：正确地接受原假设的个数（true negative）；
TP^{i, j}：正确地拒绝原假设的个数（true positive）；
FP^{i, j}：错误地拒绝原假设的个数（false positive）；
FN^{i, j}：错误地接受原假设的个数（false negative）。
这四个变量的关系如下表所示。
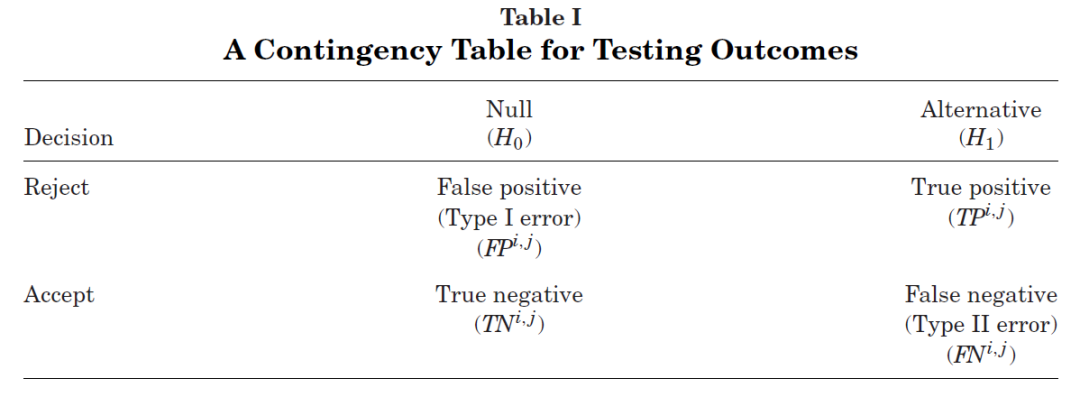
虽然 Y_i 告诉我们异象的真伪，但是为了在 Y_i 的每个 bootstrap 样本中将全部 N 个异象划分到上述四类中，需要指定用于判断的 t-statistic 阈值。例如，假设异象 A 在 Y_i 中是真实的，并假设其在 Y_i 的第 j 次 bootstrap 样本中的 t-statistic 为 2.0，小于选定的阈值（例如 2.3），因此 A 将不会被拒绝。由于 A 的原假设为假（即真异象）但它却被错误的接受，因此将被分到 FN 类。
这个例子说明，TN^{i, j}、TP^{i, j}、FP^{i, j} 以及 FN^{i, j} 四个变量是 t-statistic 阈值的函数。这是 Harvey and Liu (2020) 框架中非常关键的一点。
通过上述四个变量，Harvey and Liu (2020) 进而定义了 realized false discovery rate（RFDR）、realized rate of miss（RMISS）以及 realized ratio of false discoveries to misses（RRATIO）：
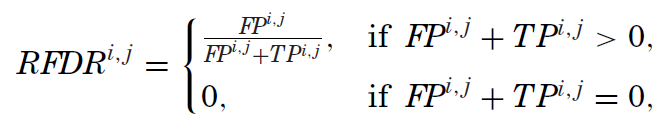
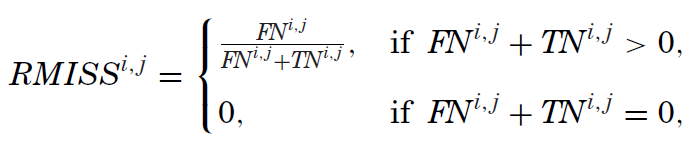
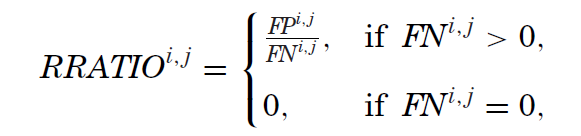
从定义不难看出，RFDR 是全部 positive 中 false positive 的占比（即所有被拒绝的原假设中，虚假异象的占比），它对应的是 Type I error；RMISS 是全部 negative 中 false negative 的占比（即所有被接受的原假设中，真实异象的占比），对应的是 Type II error；最后 RRATIO 是 false positive 和 false negative 之比，它代表了两类错误的比重。
在实际应用中，对于每一个 Y_i 进行 J 次 bootstrap sampling。假设第一轮 bootstrap 中由原始数据 X_0 一共生成了 I 个 Y_i，因此对于上述每一个变量，双重 bootstrap 都最终能够生成 I × J 个。将它们各自取平均便得到最终的 Type I error rate、Type II error rate 以及权衡两类错误之比的 ORatio（Odds）。
由于用来计算 Type I、Type II 以及 ORATIO 的变量 TN^{i, j}、TP^{i, j}、FP^{i, j} 以及 FN^{i, j} 是t-statistic 阈值的函数，因此这三个最终的变量也是 t-statistic 阈值的函数。这便让人们可以根据最关心的问题选择最合适的 t-statistic 阈值。
如果我们最关注 Type I error rate，那么可以控制其不超过给定的水平（例如 5%）并以此确定 t-statistic 阈值；如果我们更关心 Type II error rate 或者二者之间的取舍，则可以通过指定 Type II error rate 或者 ORATIO 的水平来选择适当的 t-statistic 阈值。
最后一点需要说明的是，由于这两类错误之间的取舍（即更低的 Type I error rate 意味着更高的 Type II error rate），因此当以控制 Type I error rate 不超过设定水平为目标时，Harvey and Liu (2020) 的双重 bootstrap 方法保证了求出的 t-statistic 阈值同时对应了最优的 Type II error rate。换句话说，相比于其他传统的多重假设检验方法，Harvey and Liu (2020) 的方法有更高的 power。
在 Harvey and Liu (2020) 一文中，二位作者通过大量的实证（检验异象、检验基金经理的超额收益等）来论证了新方法的先进性。感兴趣的小伙伴请阅读原文。下面来看看 A 股的实证。
03
实证
本节针对 95 个异象应用 Harvey and Liu (2020) 提出的方法（异象收益率序列来自 BetaPlus 小组）。这 95 个异象超额收益 t-statistic 的分布如下。在实证中选择 I = 100，J = 200。
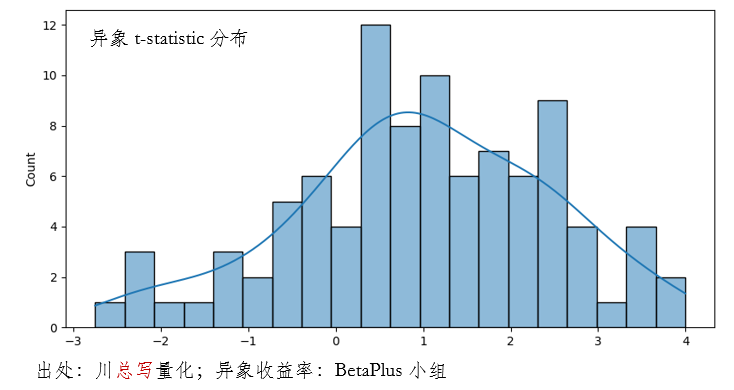
在应用中，假设 p_0 的取值范围是 0% 到 20%；例如，当 p_0 = 0% 时认为所有异象都是虚假的；当 p_0 = 20% 时认为 19 个异象是真实的。由逻辑可知，当 p_0 增大时，先验认为更多的异象是真实的，因此对于给定的 Type I error rate 水平，得到的 t-statistic 阈值会降低。实证结果符合上述预期。
下图给出了 p_0 = 0%、5%、10% 以及 20% 时 Type I、Type II、以及 ORATIO 的曲线。由前述可知，它们都是 t-statistic 阈值的函数，因此下面每个图中的横坐标都是 t-statistic 阈值。
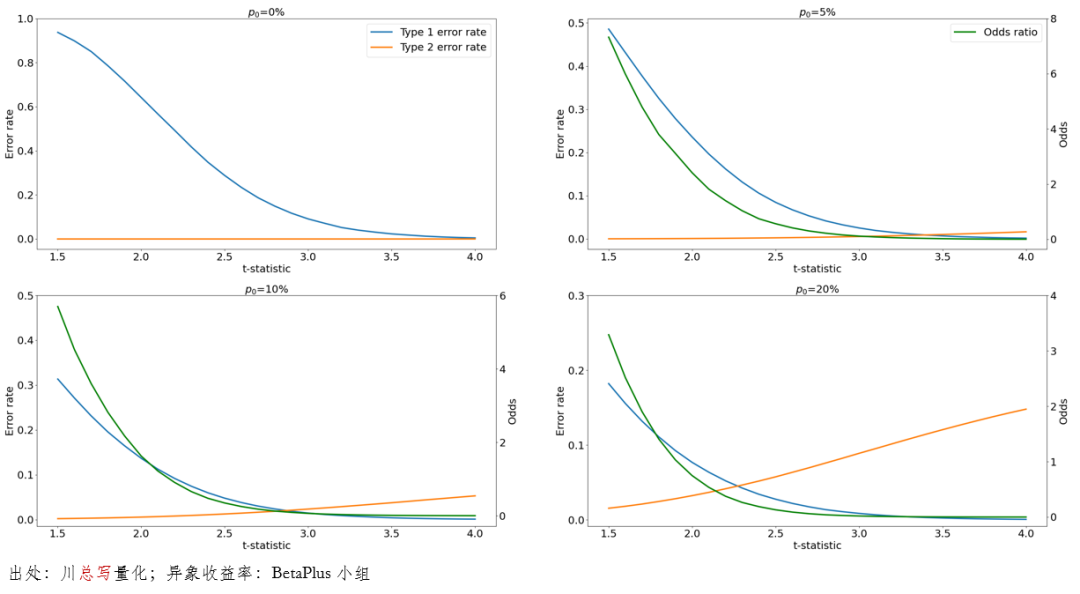
当 p_0 很高时（比如我们对于待检验的异象很有信心），Type I error rate 随 t-statistic 阈值的增大而迅速下降，与此同时 Type II error rate 则快速上升。这十分符合预期，因为当真实异象占比很高时，如果选择的 t-statistic 阈值太严苛，就很有可能错失真实的异象，即出现 Type II error。
下图给出了不同 p_0 时，控制 5% 的 Type I error rate 所需要的 t-statistic 阈值。这个图很好的表明了贝叶斯思维的重要性。在传统多重假设检验方法中，由于不指定 p_0，“正交化”会作用于所有异象，导致 t-statistic 阈值过高（对应下图中 p_0 = 0 的情况）。而当人们有足够的理由对待检验的异象给出合理的先验时，通过合适的 p_0 就能够求出更加准确的 t-statistic 阈值，从而在给定的 Type I error rate 水平下最小化 Type II error rate。
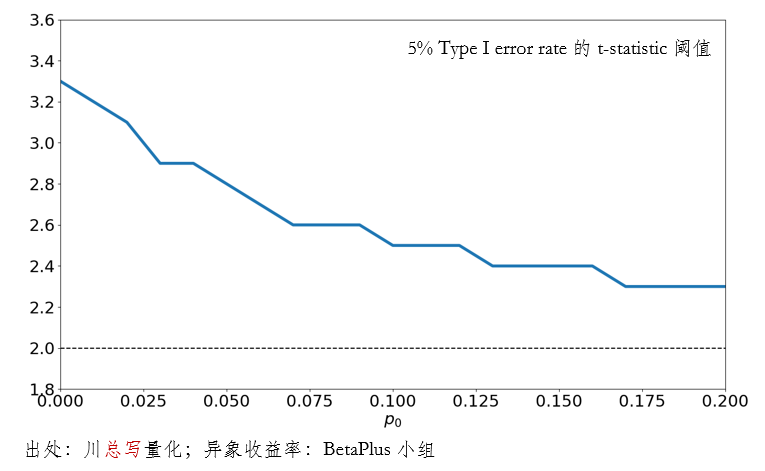
通过本节的实证可以发现，加入了贝叶斯思想（通过 p_0）和考虑了两类错误的权衡之后，Harvey and Liu (2020) 的多重假设检验方法可以找到更好的 t-statistic 阈值。
04
结语
为了从一大堆异象中找到真正的、规避虚假的，多重假设检验方法走进了人们的视线并早已被学术界广泛接受。然而传统的多重假设检验方法对原始数据的分布有不同的假设，而不同异象收益率的相关性往往不满足某些假设，使得很多方法难以应用。
本文介绍的 Harvey and Liu (2020) 框架则不受上述问题的困扰。此外，该方法通过引入 p_0 和双重 bootstrap 让人们在控制 Type I error rate 的同时也能够权衡 Type II error rate。这在 Type II error 的成本越来越高的今天显得尤为重要。
最后我想强调的是，
Harvey and Liu (2020)
的先进性和灵活性让它可以自如的应对每个具体的问题。不同的一大组异象、不同的 p_0 的选择（来自研究者的经验）、不同的分析目标（Type I vs Type II）会得到不同的 t-statistic 阈值。因此，
该框架让人们解决最关心的问题，而不是不加区分的使用某个统一的阈值（比如 3.0）。
有理由期待，该方法在未来检验异象和分析基金超额收益的场景中发挥更重要的作用。
感谢阅读。预祝各位新春快乐。
A
附录
来自 Wikipedia 的计算单一假设检验中 Type II error rate 的例子。
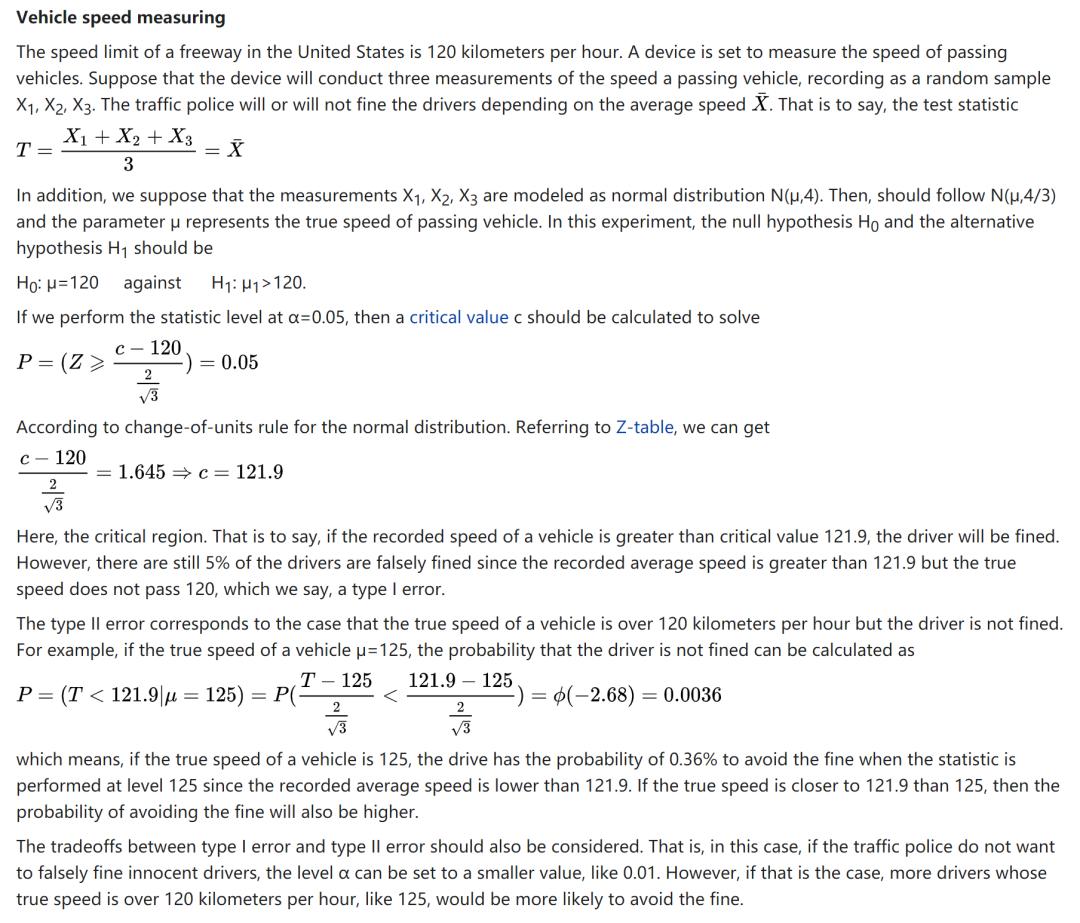
参考文献
Harvey, C. R. and Y. Liu (2020). False (and missed) discoveries in financial economics. Journal of Finance 75(5), 2503 – 2553.
Harvey, C. R., Y. Liu, and A. Saretto (2020). An evaluation of alternative multiple testing methods for finance applications.Review of Asset Pricing Studies 10(2), 199 – 248.
免责声明：入市有风险，投资需谨慎。在任何情况下，本文的内容、信息及数据或所表述的意见并不构成对任何人的投资建议。在任何情况下，本文作者及所属机构不对任何人因使用本文的任何内容所引致的任何损失负任何责任。
川总写量化
分享量化理论和实证心得
继续阅读
阅读原文