理论基础
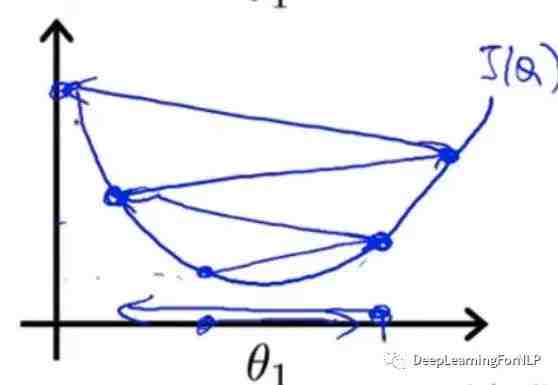
    现在比如有两个参数的损失函数
我们的目的是使之最小也就是得到能够使J函数最小的
，
，公式表示为：
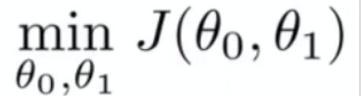
    我们画出当
取不同值时J的变化图是这样的
    颜色越深代表J值越大。
    我们比如随便取一个点(
,
各等于某值时)，此点如图所示：
    此时比如我们站在此点上，想要快速到达谷底(也就是使J函数达到极小值)。此时我们放眼望去，环望四周，很自然的向此时坡最陡的方向的下方迈上一步，接着在继续重复我们的过程，直到四周都比当下高 (此时)为止，就是走到谷底(J函数达到极小值)，完成目标。
    我们来看看我们的路线

    这时会不会有人问为什么会是极小值。
    这时我们重新找一个点
    跟上面的过程一样，我们再走一遍

    你瞅瞅，是不是到达另一个谷底。所以说，这种方法找的是
局部的最小值
，也就是
全局的极小值
。这种方法就是
梯度下降算法
。

    此时介绍梯度下降算法，简单起见，我们从一个变量开始，比如此时我们的损失函数J(
)是
    随机给
取一个值，此点如上图所示。对此点求导：
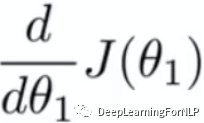
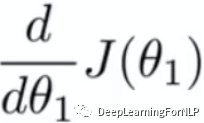
此时的导数值为正数，我们要向它的相反方向走一步，到达如图所示点
    此时的公式表达为：
为learning rate 即学习率，这里表示用来控制步伐的大小，取值范围 (0-1]   (一般取值1，0.1，0.01，0.001... 也或者0.3，0.03，0.003...根据情况而定)。
    不断的重复上面公式的过程，直到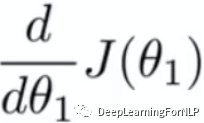
等于0或者特别小(多小，根据实际情况设定)停止。
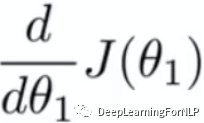
    我们再考虑随机点在左边的情况。比如取点如图所示：
    此时的J在
点的导数
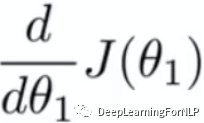为负数。
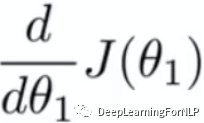
此时我们应该向右走，则此时的表达式为
更新后
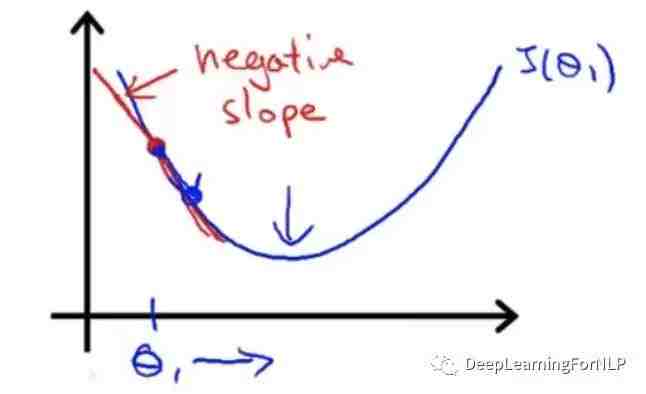
跟上面的过程一样，直到更新到导数为0或特别小为止。
由此可见，无论导数正负，表达式一样。所以我们规定梯度下降算法的更新过程就是
此时我们具体谈谈
：
取值过小，则会有这样的情况：
    到达极小值的速度特别慢。

而
取值过大，则还会有这种情况：
    永远找不到极小值。

所以如果你想在
上做优化，可以这样
在坡度大的时候取大值小的时候取小值。(根据实验情况而定)
现在我们再回归到我们的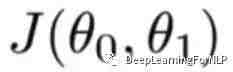
函数中来。
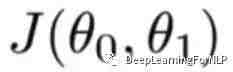
我们对它进行优化的表达式为：
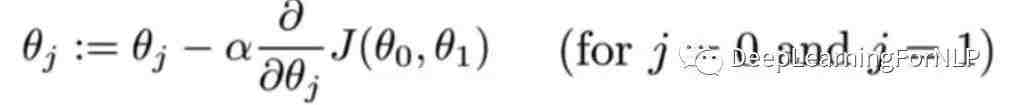
（这里是
偏导
）

这里有个误区，正确的更新过程是这样的：
等更新完再赋值。
下面的做法是错误的：
更新完的
在temp1的更新过程中被调用，此时已经不是之前的
了。切记。
代码实践
这是个拟合直线的代码实现。
我们要将数据统一收缩到 [-1 - 1] 之间。
    X  = ( X - average(X) ) / X.max
    Y  = ( Y - average(Y) ) / Y.max 
为什么要这么做呢？
  1. 因为如果不做缩小处理，在矩阵运算时，非常有可能出现无穷大或者无穷小，导致无法计算。
  2. 缩小处理可以很容易画出模拟线条。
  3. 缩小处理在计算机中处理速度更快。
我们看看图：
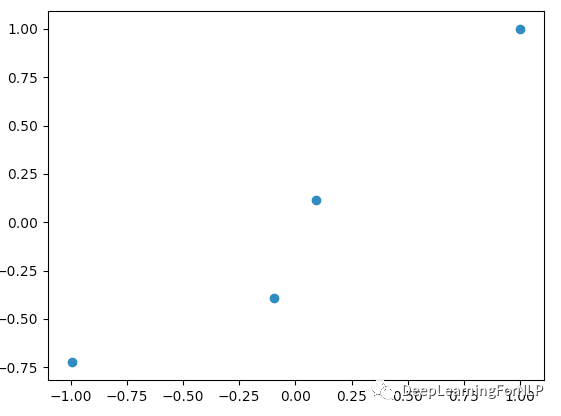
这里我设置a = 0.01是为了下面的模拟直线除数不为0设置的。一般情况下，初始化 a = b = 0。(这里a, b就是上面的
)
下面进行矩阵化：
上面图片的y1 - y4是预测值
下面代码的Y是真实值
预测值函数
拟合线段形成过程
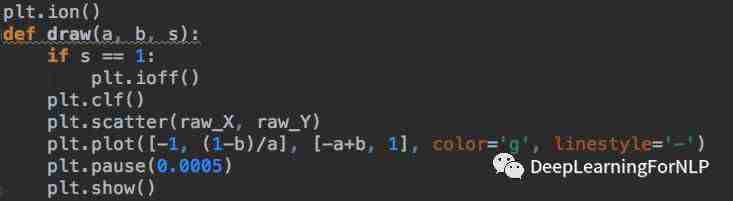
更新过程
最终的线段是
注：代码实现以上图片来自2014stanford机器学习视频
继续阅读
阅读原文