之前总是先上手一些比较高级的神经网络算法，CNN，RNN等。可是总觉得有些知识原理总是羁绊着我进一步理解。这才意识到基础的重要性。所以，就一点一点的从基础数学最小二乘法开始。这里用到的就是咱们小学或初中学到的知识。我们也都知道深度学习就是矩阵的各种计算。所以这里我们将那些知识和大学的线性代数进行简单结合。
我们先了解向量之间的投影
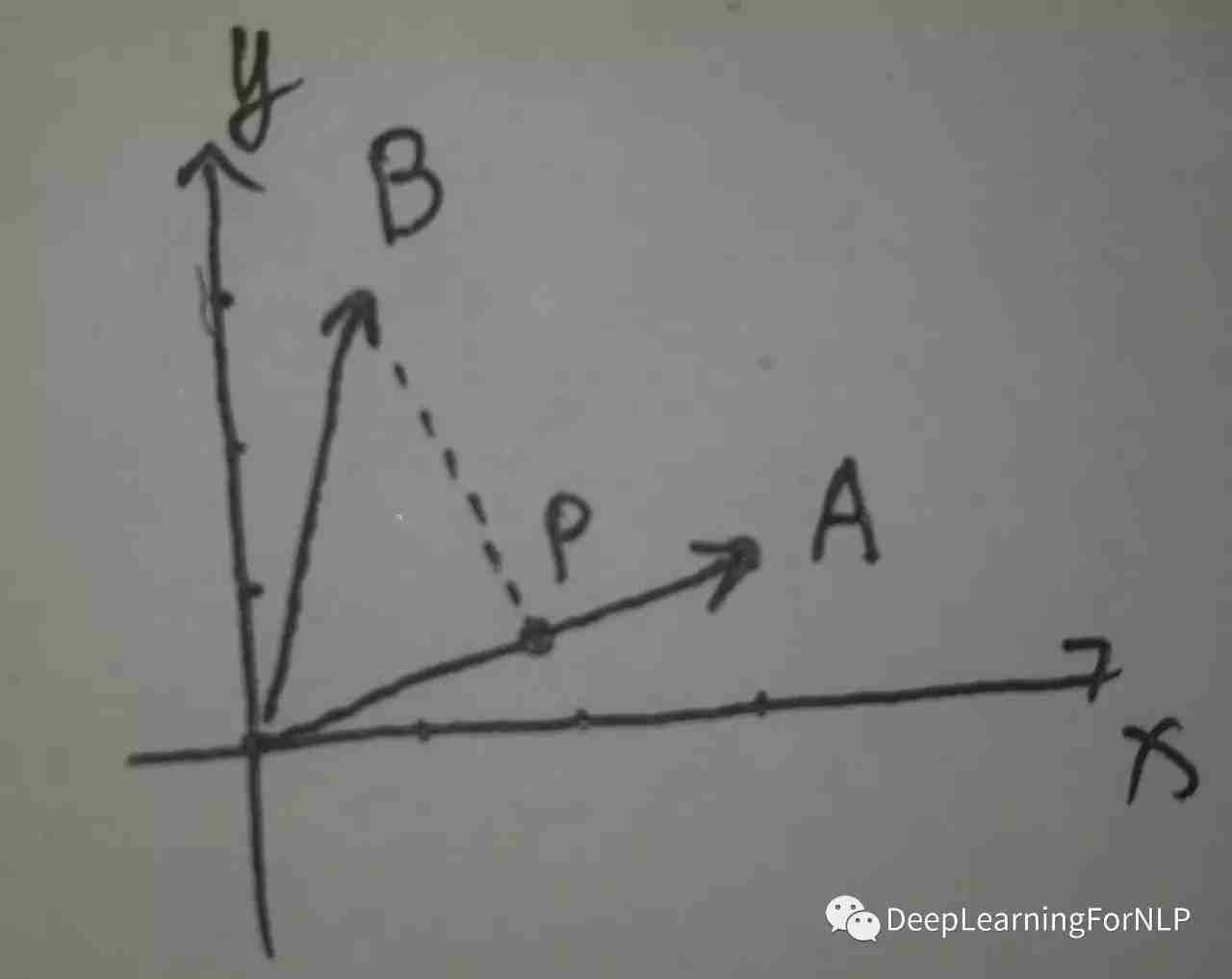
比如这张图
已知：这是2维空间，A[3, 1],  B[1, 3], 求B到A最短距离的点(也就是B到A的投影P的向量)。
我们可以先用A来表示P：P = A*x  = [3, 1].T * x   (x 是 A的线性组合的系数，是个变量，就是我们要求的实数)
若使BP距离最短，则使||P - B||^2最小就行，即 使||A*x - B||^2最小。
化解：
||A*x - B||^2 = (A*x)^2 - 2AB*x + B^2
对之求导并使之等于0，求最小值x
得：
2A^2x - 2AB = 0
即
A^2x = AB
因为这是矩阵运算，左成A^2的逆 
则写成x = (A^2)^(-1) * AB
则P = A * x = A * (A^2)^(-1) * AB   
代码实现
注意区别点乘和叉乘
import numpy as np
from matplotlib import pyplot as plt
A = np.array([[3], [1]])
B = np.array([[1], [3]])
P = A * np.linalg.inv(A.T.dot(A)) * (A.T.dot(B))
# print(P)
plt.plot(A[0], A[1], 'k-o')
plt.plot(B[0], B[1], 'r-o')
plt.plot(P[0], P[1], 'r-o')
plt.plot([B[0], P[0]], [B[1], P[1]], 'y-o')
plt.plot([0, A[0]], [0, A[1]], 'k-')
plt.ylim(0, 3)
plt.xlim(0, 3.5)
plt.text(A[0]+0.1, A[1], 'A')
plt.text(B[0], B[1]-0.1, 'B')
plt.text(P[0]+0.1, P[1]+0.1, 'P')
plt.show()
给定一堆点，求一条线来拟合这些点
比如有n个点(X1, Y1), ..., (Xn, Yn)
我们选取特征函数 y = ax^2 + bx + c  
(
特征函数的选取可以任意函数，根据经验选取特征函数，比如也可以是y = ax^2 + bx + csinx+ de^2 + f等 
)
那我们就有以下矩阵表示：
代码实现：
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(-1, 1, 100)
y = 2.3*x*x + 3.5*x + 0.04
y_ = y + np.random.rand(len(x)) - 0.5
A = []
times = 2
for i in range(times+1):
    A.append(x**(times-i))
A = np.array(A).T
B = y_.reshape(y_.shape[0], 1)
w = np.linalg.inv(A.T.dot(A)).dot(A.T).dot(B)
pred_y = A.dot(w)
print(w)
plt.scatter(x, y_)
plt.plot(x, y, 'k-')
plt.plot(x, pred_y, 'r-')
plt.show()
结果系数输出：
[[ 2.28283947]
 [ 3.46918764]
 [ 0.05473155]]
黑线为理想曲线，红色为拟合曲线。

这样看，效果还是可以的。
继续阅读
阅读原文